White Papers

Linear Regression

Linear regression is one of the prime statistical tools used to study or analyze the relationship between two variables, X and Y. The purpose of this widely used tool is to analyze the correlation of a response variable to the notified explanatory variable. This statistical method is also employed to forecast future values from past values. In economy, it is generally used to ascertain when and how the prices are extended beyond the stipulated limits. The technique applies the method of least squares in which a straight line is drawn through the variable prices. This way it lessens the yawning distance between the available prices and the sequential trendline.

How Linear Regression Works?

Linear regression usually works on logical assumptions. For example if you want to predict the next day price or demand of any particular security or commodity, then your logical guess would be quite close to the present price or demand of the same. If prices or demands are continuously soaring or slipping, then your logical guess will reflect with an upward bias or downward bias respectively. The line which is drawn to connect the two variables using the techniques of least squares is commonly known as a 'Linear Regression trendline'. It is a line which is shown exactly at middle of the demands or prices.

The main and foremost purpose of linear regression is to adapt the slope values to that of the variables and then form the line that predicts Y from X in best perceivable manner. If narrowed down, the main goal of this technique is to condense the total number of squares of the vertical distances of the variables from the prediction line.

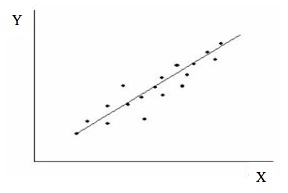
In the above figure, a correlation displayed in a straight line is based on the assumption of two variables, X and Y. Though the exact values cannot be figured out through the values of Y for different values of X, but with 'Linear regression Analytics Outsourcing', you can assume the statistical correlation between these two variables.

There are various statistics software like SAS, SPSS and R-square that are commonly used in linear regression analyzes.

SPSS

In SPSS, while deciding to analyze the data through linear regression, you must first be assured if the data you are going to analyze can be analyzed using the same or not. Then follows checking if the incoming data passes six assumptions or not, which are required for this technique to bear correct result. Here is the lowdown of the assumptions

• Both of the variables must be measured at continuous intervals or ratio levels.
• A linear correlation should exist between both the points. You can also create scatterplot joining the dependent variables with that of the independent ones.
• There should not a single trail of any outliers since they have huge impact on scatterplots. Outliers are single data points within the data that depicts a slight variation from the usual pattern.
• The observations must be independent which can be checked further using Durbin-Watson statistic.
• The data should reflect homoscedasticity, according to which the variances will be similar as you move along any peculiar line.
• Lastly, make it sure that the residual errors of the variables are distributed on normal basis. To check this you can either use a Histogram or a normal P-P Plot.

R-Square

Also termed as coefficient of determination, R-square is the most commonly used statistic which is used to evaluate any given regression equation. Value of R-square can range from 0.0 to 1.0. This value can be further multiplied by 100 in order to acquire a percentage of the variance.

Unlike SPSS, there are only four main assumptions in case of R-square. These assumptions must be complied with, in order to conduct a linear regression analysis. These are linearity, normality, independence and homoscedasticity.

SAS

SAS is the most fully featured statistical package that runs on a vast variety of platforms including Windows and Unix. Hence, it is also the most sought after software used for linear regression. Peculiar concepts of linear regression like simple and multiple regression, and regression with categorical predictors are covered in SAS. The software comprises additional coding systems for categorical variables in regression analysis. Moreover, it takes place in-depth interactions of continuous and categorical variables.